NOIP2009普及 T4 道路游戏

~{→看不见LaTex格式的Dalao们请刷新本页Thanks♪(･ω･)ﾉ←}~

[NOIP2009普及]T4 道路游戏

题面

小新正在玩一个简单的电脑游戏。

游戏中有一条环形马路，马路上有 $n$ 个机器人工厂，两个相邻机器人工厂之间由一小段马路连接。小新以某个机器人工厂为起点，按顺时针顺序依次将这 $n$ 个机器人工厂编号为$1−n$，因为马路是环形的，所以第$n$个机器人工厂和第$1$个机器人工厂是由一段马路连接在一起的。小新将连接机器人工厂的这 $n$ 段马路也编号为 $1−n$，并规定第 $i$ 段马路连接第 $i$ 个机器人工厂和第 $i+1$ 个机器人工厂（$1≤i≤n-1$），第 $n$ 段马路连接第 $n$ 个机器人工厂和第$1$个机器人工厂。

游戏过程中，每个单位时间内，每段马路上都会出现一些金币，金币的数量会随着时间发生变化，即不同单位时间内同一段马路上出现的金币数量可能是不同的。小新需要机器人的帮助才能收集到马路上的金币。所需的机器人必须在机器人工厂用一些金币来购买，机器人一旦被购买，便会沿着环形马路按顺时针方向一直行走，在每个单位时间内行走一次，即从当前所在的机器人工厂到达相邻的下一个机器人工厂，并将经过的马路上的所有金币收集给小新，例如，小新在 $i$（$1≤i≤n$）号机器人工厂购买了一个机器人，这个机器人会从i号机器人工厂开始，顺时针在马路上行走，第一次行走会经过i号马路，到达 $i+1$号机器人工厂（如果$i=n$，机器人会到达第$1$个机器人工厂），并将$i$号马路上的所有金币收集给小新。游戏中，环形马路上不能同时存在$2$个或者$2$个以上的机器人，并且每个机器人最多能够在环形马路上行走$p$次。小新购买机器人的同时，需要给这个机器人设定行走次数，行走次数可以为 $1$~$p$ 之间的任意整数。当马路上的机器人行走完规定的次数之后会自动消失，小新必须立刻在任意一个机器人工厂中购买一个新的机器人，并给新的机器人设定新的行走次数。

以下是游戏的一些补充说明：

游戏从小新第一次购买机器人开始计时。
购买机器人和设定机器人的行走次数是瞬间完成的，不需要花费时间。
购买机器人和机器人行走是两个独立的过程，机器人行走时不能购买机器人，购买完机器人并且设定机器人行走次数之后机器人才能行走。
在同一个机器人工厂购买机器人的花费是相同的，但是在不同机器人工厂购买机器人的花费不一定相同。
购买机器人花费的金币，在游戏结束时再从小新收集的金币中扣除，所以在游戏过程中小新不用担心因金币不足，无法购买机器人而导致游戏无法进行。也因为如此，游戏结束后，收集的金币数量可能为负。

现在已知每段马路上 $m$ 个单位时间后，扣除购买机器人的花费，小新最多能收集到多少金币。

Input

第一行 $3$ 个正整数$n,m,p$，意义如题目所述。

接下来的$n$行，每行有 $m$ 个正整数，每两个整数之间用一个空格隔开，其中第 $i$ 行描述了 $i$ 号马路上每个单位时间内出现的金币数量（$1≤金币数量≤100$），即第 $i$ 行的第 $j$（$1≤j≤m$）个数表示第 $j$ 个单位时间内 $i$ 号马路上出现的金币数量。

最后一行，有 $n$ 个整数，每两个整数之间用一个空格隔开，其中第 $i$ 个数表示在 $i$ 号机器人工厂购买机器人需要花费的金币数量（$1≤金币数量≤100$）。

Output

共一行，包含 $1$ 个整数，表示在 $m$ 个单位时间内，扣除购买机器人

花费的金币之后，小新最多能收集到多少金币。

Sample Input

2 3 2
1 2 3
2 3 4
1 2

Sample Output

Hint

【数据范围】

对于 40%的数据，$2≤n≤40,1≤m≤40$。

对于 90%的数据，$2≤n≤200,1≤m≤200$。

对于 100%的数据，$2≤n≤1000,1≤m≤1000,1≤p≤m$。

题解

我们在做此题之前，先将环的标号标为$0$~$n-1$以便于取模直接处理。

我们先来手推一波样例（$t_{i,j}$表示第i条路在第j个单位时间的价值，路边的×n代表该条路会被经过n次，我们给第一个机器人设定2个单位时间，第二个机器人设定1个单位时间）：

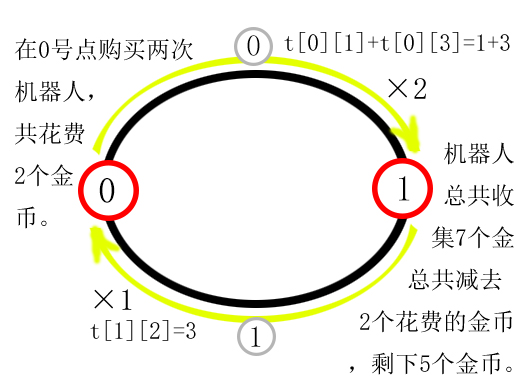
我们用$f_i$表示在第$i$个单位时间的最大金币数，$cost_i$代表第$i$个工厂买机器人的钱，$val_{i,j}$代表在第$i$个时刻到达$j$号工厂的价值，$sum_{i,j}$为其前缀和。

我们先将节点编号为0~n-1。

由于第$i$条路指向第$i+1$号工厂，那么，我们不妨直接把第$i$条路的价值变成第$i+1$号工厂的价值。

因为价值受到工厂序号和单位时间这两个约束限制，我们对价值进行二维前缀和处理，我们可以在当前机器人始末进行差分处理，求出总共经过的路的取得的价值。

先从$O(n^3)$说起。

首先，我们可以写出一个$dp$方程来：

$f_i=Max(f_{i-k}+sum_{i,j}-sum_{i-k,j-k}-cost_{j-k})$

机器人从$j-k$号工厂出发，走$k$个时间单位在$i$个时间单位走到$j$号工厂，求出$Max(f)$。

唔，其实如果考试时间不够，我觉得对于$n\le 200$的数据完全没有问题，想想你已经拿到了$90$分。

但是对于练题来说，我们应该去想想1000的数据：

emmm，$i,j$固定，只在枚举$k$时，好像$sum[i][j]$不会改变，先拿出来再说。

$f_i=Max(f_{i-k}-sum_{i-k,j-k}-cost_{j-k})+sum_{i,j}$

我们其实可以发现：

$f_{i-k}-sum_{i-k,j-k}-cost_{j-k}$中，我们各项随着$k$的改变而变动，那么由于所有的下标都同时减$k$其实就是在二维前缀$sum$的对角线上取$f_{i-k}-sum_{i-k,j-k}-cost_{j-k}$整体的最大值。

ok，那么直接用堆来维护这一坨的最大值吧！好像这样复杂度就降为了$O(n^2logn)$，足以过这题了。

Code

1
2