二分图专题

发表于 | 分类于 | ℃热度
~{→看不见LaTex格式的Dalao们请刷新本页Thanks♪(･ω･)ﾉ←}~

我对二分图简直自闭，决定再次学习一波，唉。

一、二分图的定义

  • 简单的说，如果图中的点可以被分为两组，并且所有的边的两端不在同一组内，也就是说都连通两个组，那么这就是一个二分图。

  • 二分图还有另一个定义，如果把一个图的顶点划分为两个不相交集，使每一条边分别连接两集中的顶点，那么这就是一个二分图。

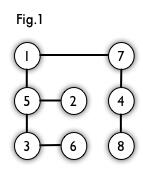
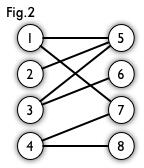
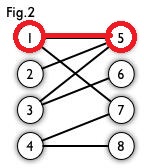
Fig1是一个二分图，看起来不方便，就画成Fig2。

二、匹配的定义

  • 简单地说，就是一个边集，且满足其中任意两边都没有公共顶点。

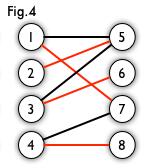
如图，Fig3、Fig4是Fig2 的匹配：

imgimgimgimg

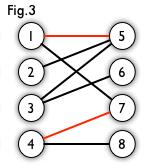
  • 匹配中还有一些定义：匹配点，匹配边，未匹配点，非匹配边。比如Fig3中的1,4,5,7是匹配点，1-5,4-7是匹配边。

  • 最大匹配：一个图的所有匹配中，所含匹配边最多的匹配，称为该图的最大匹配。Fig4是一个最大匹配。

  • 完美匹配：如果一个匹配内，所有的点都是匹配点，那么这个匹配就是一个完美匹配，显然有，完美匹配一定是最大匹配。但是并不是所有的图都存在完美匹配。

三、另一些定义（匈牙利算法）

  • 交替路：从一个未匹配点出发，依次经过非匹配边，匹配边，非匹配边，匹配边……如此形成的路径叫交替路。

  • 增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点，但不能算出发点，那么这条路叫做增广路。如图，Fig5中的增广路为Fig6：

    imgimg

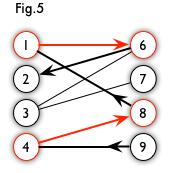
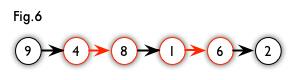
  • 增广路有一个特点：非匹配边一定比匹配边多一条。

  • → 由此，只要把增广路中的匹配边和非匹配边身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数比原来多1条，其实如果交替路以非匹配点结束，那么该交替路就是一条增广路。

四、匈牙利算法

  • 1、基本思想：

    通过寻找增广路，把增广路的匹配边和非匹配边身份交换，多出一条匹配边，直到不能找到增广路为止。

    Code：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    #include<bits/stdc++.h>
    #define MAXN 9999
    using namespace std;
    int nx,ny;//nx表示二分图左边顶点的个数，ny表示二分图右边顶点的个数
    int m;//m代表边的条数
    int cx[MAXN],cy[MAXN];//如果有cx[i]=j，则必有cy[j]=i，说明i点和j点能够匹配
    int x,y;//x点到y点有边
    int e[MAXN][MAXN];//邻接矩阵
    int visited[MAXN];//标记数组，标记的永远是二分图右边的顶点
    int ret;//最后结果
    int point(int u)//这个函数的作用是寻找增广路和更新cx，xy数组，如果找到了增广路，函数返回1，找不到，函数返回0。
    {
        for(int v=1;v<=ny;v++)//依次遍历右边的所有顶点
        {
            if(e[u][v]&&!visited[v])//条件一：左边的u顶点和右边的v顶点有连通边，条件二：右边的v顶点在没有被访问过，这两个条件必须同时满足
            {
                visited[v]=1;//将v顶点标记为访问过的
                if(cy[v]==-1||point(cy[v]))//条件一：右边的v顶点没有左边对应的匹配的点，条件二：以v顶点在左边的匹配点为起点能够找到一条增广路（如果能够到达条件二，说明v顶点在左边一定有对应的匹配点）。
                {
                    cx[u]=v;//更新cx，cy数组
                    cy[v]=u;
                    return 1;
                }
            }
        }
        return 0;//如果程序到达了这里，说明对右边所有的顶点都访问完了，没有满足条件的。
    }
    int main()
    {
        while (cin>>m>>nx>>ny)
        {
            memset(cx,-1,sizeof(cx));//初始化cx，cy数组的值为-1
            memset(cy,-1,sizeof(cy));
            memset(e,0,sizeof(e));//初始化邻接矩阵
            ret=0;
            while (m--)//输入边的信息和更新邻接矩阵
            {
                cin>>x>>y;
                e[x][y]=1;
            }
            for(int i=1;i<=nx;i++)//对二分图左边的所有顶点进行遍历
            {
                if(cx[i]==-1)//如果左边的i顶点还没有匹配的点，就对i顶点进行匹配
                {
                    memset(visited,0,sizeof(visited));//每次进行point时，都要对visited数组进行初始化
                    ret+=point(i);//point函数传入的参数永远是二分图左边的点
                }
            }
            cout<<ret<<endl;
        }
     
    }
    //%%%%%%%%%%%%
    //来自csdn--栾琪
    //%%%%%%%%%%%%

  • 2、分析

    我们拿出Fig2来分析一波：

    img

    分析一下$point()$函数的运行过程，第一次以$1$顶点为起点进入$point(1)$函数，然后5号顶点满足条件，更新$cx[1]，cy[5]$，返回$1$。此时$1→5$这条边为匹配边，$1$号，$5$号顶点为匹配顶点。

    img

    然后以$2$顶点为其实点进入$point(1)$函数，然后访问到$5$号节点，然后以$5$号节点的匹配点$1$号节点为起始点再次进入$point(2)$函数，找到了$7$号点，这时说明找到了增广路，然后更新$cx[1],cy[7]$，然后返回$1$，更新$cx[2],cy[5]$，返回$1$，函数结束。

    img

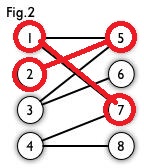
    然后以$3$号顶点为起始点进入$point(1)$函数，然后访问到$5$号节点，然后以$5$号节点的匹配点$2$号节点为起始点再次进入$point(2)$函数，找不到点了，返回$0$，到达$point(1)$函数，继续访问其他的节点。然后访问到$6$号顶点，满足条件，更新$cx[3],cy[6]$，返回$1$，函数结束。

    img

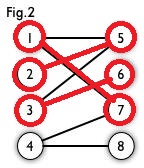
    然后以$4$号顶点为起始点进入$point(1)$函数，然后访问到$7$号节点，然后以$7$号节点的匹配点$1$号节点为起始点再次进入$point(2)$函数，然后找到$5$号节点，然后以$5$号节点的匹配点$2$号节点为起始点再次进入$point(3)$函数，找不到点了，返回$0$，到达$point(2)$函数，继续访问其他的节点，没有点了，返回$0$，到达$point(1)$函数，继续访问其他的节点，到达了$8$号节点，满足，然后更新$cx[4],cy[8]$，返回$1$，函数结束。

    img

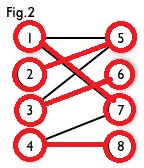
    这样我们就找到了所有的匹配边。

五、KM算法

见blog:

https://www.cnblogs.com/wenruo/p/5264235.html

https://www.cnblogs.com/logosG/p/logos.html?tdsourcetag=s_pcqq_aiomsg

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include<algorithm>
#include<iostream>
#include<limits.h>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define INT 9654234
#define mod 1000000007
typedef long long ll;
using namespace std;
const int MAXN = 305;
int N;
int ex_gir[MAXN];//每个妹子的期望值
int ex_boy[MAXN];//每个男生的期望值
bool vis_gir[MAXN];//记录每一轮匹配过的女生
bool vis_boy[MAXN];//记录每一轮匹配过的男生    每进行新的一轮，都要重新初始化这两个数组
int match[MAXN];//match[i]代表和i男生匹配的女生的编号
int slack[MAXN];//slack[i]代表i男生如果要获得女生的芳心，至少需要增加的期待值
int love[MAXN][MAXN];//记录每个妹子和男生的好感度
bool dfs(int gir)//dfs函数求的是编号为gir的女孩能否匹配到男生，如果能，返回true，否则，返回false
{
    vis_gir[gir]=true;//标记
    for(int i=1;i<=N;i++)
    {
        if(vis_boy[i])//我们规定每次匹配对于某个男生只访问一遍，如果先前访问过了，就换个男生
            continue ;
        int gap=ex_gir[gir]+ex_boy[i]-love[gir][i];
        if(gap==0)//如果这个条件满足，说明编号为gir女孩和编号为i的男孩可能能够匹配成功
        {
            vis_boy[i]=true;//标记
            if(match[i]==-1||dfs(match[i]))//如果这两个条件满足其中一个，说明编号为gir女孩和编号为i的男孩匹配成功
            {
                match[i]=gir;
                return true;
            }
        }
        else
            slack[i]=min(slack[i],gap);//如果gap不等于0，说明当前状态编号为gir女孩和编号为i的男孩不可能匹配成功，更新slack[i]。
    }
    return false;
}
int km()
{
    memset(match,-1,sizeof(match));
    memset(ex_boy,0,sizeof(ex_boy));
    for(int i=1;i<=N;i++)
        for(int j=1;j<=N;j++)
            ex_gir[i]=max(love[i][j],ex_gir[i]);//初始化ex_gir数组
    for(int i=1;i<=N;i++)
    {
        fill(slack,slack+N+1,INT);
        while (1)//这个while循环结束的条件是直到让编号为i的女生找到可以匹配的男生后
        {
            memset(vis_gir,false,sizeof(vis_gir));
            memset(vis_boy,false,sizeof(vis_gir));
            if(dfs(i))//如果这个条件满足，说明编号为i的女生找到了匹配的男生，换下一个女生,如果这个条件不满足，说明这个女生没有匹配到男生，让这个女生降低期望值后继续匹配
                break ;
            int t=INT;
            for(int j=1;j<=N;j++)//寻找在这一轮匹配中没有匹配到的男生如果要获得女生芳心所需要增加的期待值的最小值
                if(!vis_boy[j])
                    t=min(t,slack[j]);
            for(int i=1;i<=N;i++)//让在这一轮匹配中匹配过的女生的期待值减小，匹配过的男生的期待值增加
            {
                if(vis_gir[i])
                    ex_gir[i]-=t;
                if(vis_boy[i])
                    ex_boy[i]+=t;
                else
                    slack[i]-=t;//因为有些女生的期待值减小了，所以这一轮没有被匹配过的男生得到女生的芳心所需要增加的期待值就变小了，所以slack数组中的相应的值要变小
            }
        }
    }
    int res=0;//计算好感和
    for(int i=1;i<=N;i++)
        res+=love[match[i]][i];
    return res;
}
int main()
{
    cin>>N;
    for(int i=1;i<=N;i++)
        for(int j=1;j<=N;j++)
            cin>>love[i][j];
    cout<<km()<<endl;
}
//%%%%%%%%%%%%
//来自csdn--栾琪
//%%%%%%%%%%%%

六、Gale-Shapley—-婚姻匹配算法算法

见blog:

https://blog.csdn.net/Air_hjj/article/details/70828937

https://blog.csdn.net/lc_miao/article/details/78116064

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
#define MAXN 1000
typedef long long ll;
using namespace std;
int ManArray[MAXN][MAXN],GirArray[MAXN][MAXN];//ManArray[i][j]代表编号为i的男生的第j位心仪女生是几号,GirArray[i][j]代表编号为i的女生的第j位心仪男生是几号
int Man[MAXN],Gir[MAXN];//Man[i]代表i号男生所匹配到的女生是几号，Gir[i]代表i号女生所匹配到的男生是几号
int ManStarPos[MAXN];//ManStarPos[i]代表i号男生现在匹配到的女生是他心目中的第几号心仪女生
int n;
stack < int >q;//始终存放没有匹配成功的男生的编号
int GetPositionFromLaday(int GirI,int ManI)//这个函数求的是编号为ManI的男生在编号为GirI的女生的心中的排名顺序
{
    for(int i=0;i<n;i++)
        if(GirArray[GirI][i]==ManI)
            return i;//返回这个顺序
    return -1;
}
void ManLookGir(int ManI)//为编号为ManI的男生匹配女生
{
    int NowGir=ManArray[ManI][ManStarPos[ManI]];//得到这个男生应该匹配的女生的编号
    if(Gir[NowGir]==-1)//如果这个条件满足，说明这个女生没有和她对应匹配的男生，那么就匹配上
    {
        Man[ManI]=NowGir;
        Gir[NowGir]=ManI;
    }
    else//这个女生现在已经有男朋友了
    {
        int OldMan=GetPositionFromLaday(NowGir,Gir[NowGir]);//得到现男友在这个女孩心中的排名
        int NowMan=GetPositionFromLaday(NowGir,ManI);//得到我们要匹配的男生在这个女孩心中的排名
        if(OldMan<NowMan)//如果这个条件满足，说明这个女孩的现男友在这个女孩心中的排名要高于我们要匹配的这个男生的排名，这个女孩不换男朋友
        {
            ManStarPos[ManI]++;
            q.push(ManI);
        }
        else//这个女孩更喜欢我们要匹配的这个男生，换男朋友
        {
            ManStarPos[Gir[NowGir]]++;//这是一个优化
            q.push(Gir[NowGir]);
            Man[ManI]=NowGir;
            Gir[NowGir]=ManI;
        }
    }
}
int main()
{
    cin>>n;
    memset(Man,-1,sizeof(Man));//初始化这三个数组
    memset(Gir,-1,sizeof(Gir));
    memset(ManStarPos,0,sizeof(ManStarPos));
    for(int i=0;i<n;i++)//输入每个男生心目中对女生的排序
        for(int j=0;j<n;j++)
            cin>>ManArray[i][j];
    for(int i=0;i<n;i++)//输入每个女生心目中对男生的排序
        for(int j=0;j<n;j++)
            cin>>GirArray[i][j];
    for(int i=0;i<n;i++)//刚开始对每个男生都进行一次匹配，从每个男生最心仪的女生开始匹配。如果从程序这个地方进入ManLookGir函数，那么每个男生都会和自己最心仪的女生进行一次匹配，因为是ManStarPos数组决定的，至于能否匹配成功，这就不一定了
        ManLookGir(i);
    while(!q.empty())
    {
        int i=q.top();
        q.pop();
        ManLookGir(i);
    }
    for(int i=0;i<n;i++)
        cout<<"Man NO.: "<<i<<" Laday NO.: "<<Man[i]<<endl;
}
//%%%%%%%%%%%%
//来自csdn--栾琪
//%%%%%%%%%%%%

什么？你说为什么我后面都没了？都只挂了一个（不不不，其实是两个）博客地址呢？

那还用说！我不会啊_(¦3」∠)_

-------------本文结束(づ￣ 3￣)づ~感谢您的阅读(*╹▽╹*)-------------