CodeForces#715 C.Digit Tree

~{→看不见LaTex格式的Dalao们请刷新本页Thanks♪(･ω･)ﾉ←}~

2019寒假集训题

E.Digit Tree

题面

ZS the Coder has a large tree. It can be represented as an undirected connected graph of $n$ vertices numbered from $0$ to $n - 1$ and $n - 1$ edges between them. There is a single nonzero digit written on each edge.

One day, ZS the Coder was bored and decided to investigate some properties of the tree. He chose a positive integer $M$, which is coprime to $10$, $i.e$. $gcd(M,10)=1$.

ZS consider an ordered pair of distinct vertices $(u, v)$ interesting when if he would follow the shortest path from vertex $u$ to vertex $v$ and write down all the digits he encounters on his path in the same order, he will get a decimal representaion of an integer divisible by $M$.

Formally, ZS consider an ordered pair of distinct vertices $(u, v)$ interesting if the following states true:

• Let $a_1 = u, a_2, …, a_k = v$ be the sequence of vertices on the shortest path from $u$ to $v$ in the order of encountering them;
• Let $d_i$ ($1 ≤ i < k$) be the digit written on the edge between vertices $a_i$ and $a_i$ + 1;
• The integer $\overline{d_1d_2d_3…d_{k-1}}=\sum_{i=1}^{k-1}d_i·10^{k-1-i}$ is divisible by $M$.

Help ZS the Coder find the number of interesting pairs!

---

简要翻译

给定一个有$N$个点的树，问其中有多少条路径满足他们的边权连成的数对$M$取余为$0$。

其中$gcd(M,10)=1$。

---

Input

第一行包含两个整数$n$和$M$。

下面包含$n-1$行，每行包含$3$个整数。第$i$行包含$u_i,v_i,w_i$分别代表一条边的出点，入点，权值。

---

Output

输出一行一个整数表示数对个数。

---

Sample Input 1

6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7

---

Sample Output 1

7

---

Sample Input 2

5 11
1 2 3
2 0 3
3 0 3
4 3 3

---

Sample Output 2

8

---

Hint

$2\le n\le 100,000,1\le M\le 10^9,gcd(M,10)=1$。

$0\le u_i,v_i\le n,1\le w_i\le 9$。

---

Sample Explain

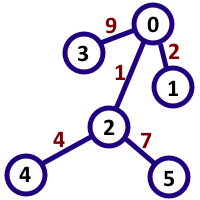
在第一个例子中，所求数对是$(0,4),(1.2),(1.5),(3,2),(2.5),(5,2),(3,5)$，由这些数对组成的数分别是$14,21,217,91,7,7,917$，都是$7$的倍数。注意$(2,5)$和$(5,2)$是不同的数对。

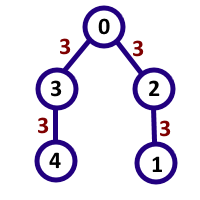
在第二个例子中，所求数对是$(4,0),(0,4),(3,2),(2,3),(0,1),(1,0),(4,1),(1,4)$，其中6对给出了数字$33$而其中$2$对给出了数字$3333$，它们都是$11​$的倍数。

---

我们点分治套路一波。

然后分析一下如何统计答案。

对于$x→y$的路径，等价于$x→root→y$，我们要处理出$dis[x]$和$dis[y]$分别表示$x$到$root$,$root$到$y$连成的数对$mod$取模后的结果。

在合并时，我们知道，如果路径是合法的，那么肯定满足$dis[x]×10^{deep[y]}+dis[y]≡0\ \pmod{M}​$

也就是$dis[x]≡-dis[y]×10^{-deep[y]}\pmod{M}$

用$dfs​$来统计答案即可。

---

Code

//本代码来自"睿智"的大佬yyd，本蒟蒻太菜被他踩爆了，本博客右侧有他的博客地址yo~
#include<bits/stdc++.h>
using namespace std;

inline int read()
{
    int N=0,C=0;char tf=getchar();
    for(;!isdigit(tf);tf=getchar())C|=tf=='-';
    for(;isdigit(tf);tf=getchar())N=(N<<1)+(N<<3)+(tf^48);
    return C?-N:N;
}

const int N=100010,INF=0x7fffffff;
int n,p,m,x,y,z;
int siz[N],mx[N],rt,All,dep[N];
long long a[N],P[N],ans;
pair<long long,long long>b[N];//< b ,deep >
pair<long long,long long>g[N];//< rt->x ,x->rt >
int len,lin[N];
struct nc{int y,nxt,v;}e[N<<1];
bool v[N];

#define fi first
#define se second
#define mp make_pair

inline void ins(int x,int y,int v)
{
	e[++len].nxt=lin[x];
	lin[x]=len;
	e[len].y=y;
	e[len].v=v;
}

void exgcd(int a,int b,int &x,int &y)
{
	if(!b){x=1,y=0;return;}
	exgcd(b,a%b,y,x);
	y-=a/b*x;
}

inline int inv(int a)
{
	int x,y;
	exgcd(a,p,x,y);
	return (x%p+p)%p;
}

void dfs_rt(int x,int f)
{
	siz[x]=1,mx[x]=0;
	for(int i=lin[x];i;i=e[i].nxt)
	{
		int y=e[i].y;
		if(y==f||v[y])continue;
		dfs_rt(y,x);
		siz[x]+=siz[y];
		mx[x]=max(mx[x],siz[y]);
	}
	mx[x]=max(mx[x],All-siz[x]);
	if(mx[x]<mx[rt])rt=x;
}

void dfs_ab(int x,int f)
{
	a[++m]=g[x].se,b[m]=mp(g[x].fi,dep[x]);
	for(int i=lin[x];i;i=e[i].nxt)
	{
		int y=e[i].y;
		if(y==f||v[y])continue;
		dep[y]=dep[x]+1;
		g[y]=mp((g[x].fi*10+e[i].v)%p,(g[x].se+P[dep[x]]*e[i].v)%p);
		dfs_ab(y,x);
	}
}

inline void cal(int x,int c)
{
	sort(a+1,a+m+1);
	for(int i=1;i<=m;++i)
	{
		long long aa=1LL*(p-b[i].fi)*inv(P[b[i].se])%p;
		ans+=(upper_bound(a+1,a+m+1,aa)-lower_bound(a+1,a+m+1,aa))*c;
	}
}

void solve(int x)
{
	v[x]=1,dep[x]=0;
	g[x].fi=g[x].se=0;
	m=0,dfs_ab(x,0),cal(x,1);//多算一个 x->x 
	
	for(int i=lin[x];i;i=e[i].nxt)
	{
		int y=e[i].y;
		if(v[y])continue;
		dep[y]=1,g[y].fi=g[y].se=e[i].v;
		m=0,dfs_ab(y,0),cal(y,-1);//减去子数内答案 
		
		All=siz[y],rt=0,dfs_rt(y,0);
		solve(rt);//点分治 
	}
}

int main()
{
	n=read(),p=read(),P[0]=1;
	for(int i=1;i<n;++i)
	{
		x=read()+1,y=read()+1,z=read()%p;
		ins(x,y,z),ins(y,x,z);
		P[i]=P[i-1]*10%p;
	}
	
	mx[0]=INF,All=n,dfs_rt(1,0),solve(rt);
	printf("%lld\n",ans-n);
	
    return 0;
}