~{→看不见LaTex格式的Dalao们请刷新本页Thanks♪(･ω･)ﾉ←}~

2019寒假集训题

A.XOR on Segment

题面

You’ve got an array $a$ , consisting of $n$ integers $a_1$,$a_2$,…,$a_n$. You are allowed to perform two operations on this array:

Calculate the sum of current array elements on the segment $[l,r]$ , that is, count value $a_l+a_{l+1}+…+a_r$ .
Apply the $xor$ operation with $a$ given number $x$ to each array element on the segment $[l,r]$ , that is, execute 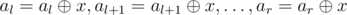. This operation changes exactly $r-l+1$ array elements.

Expression 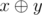means applying bitwise xor operation to numbers $x$ and $y$ . The given operation exists in all modern programming languages, for example in language $C++$ and Java it is marked as “^”, in Pascal — as “$xor$”.

You’ve got a list of m m m operations of the indicated type. Your task is to perform all given operations, for each sum query you should print the result you get.

简要翻译

给定一个长为$n$($n\leq10^5$)的数组

数组里的数不超过$10^6$

有两种操作：

1:求$sum[l,r]$;

2:对$[l,r]$中的所有数和$x$异或

Input

第一行包含一个整数$n$，表示数组的长度。

第二行包含用空格隔开的$n$个整数，$a_1,a_2,a_3,…,a_n$表示数组。

第三行包含一个整数$m$，表示操作的个数。

下面包含$m$行，每行包含一个整数$t_i$，表示操作的类型。

当$t_i=1$时，之后包含2个整数$l,r$，求$sum[l,r]$。
当$t_i=2$时，之后包含3个整数$l,r,x$，对$[l,r]$的数与$x$进行异或操作。

Output

对于每个操作$1$，输出一行一个整数代表答案。

请不要使用”$\%lld$”去读入或输出$long\ long$；

你最好使用”$cin$,$cout$”或者”$\%I64d$”。

Sample Input 1

5
4 10 3 13 7
8
1 2 4
2 1 3 3
1 2 4
1 3 3
2 2 5 5
1 1 5
2 1 2 10
1 2 3

Sample Output 1

Sample Input 2

6
4 7 4 0 7 3
5
2 2 3 8
1 1 5
2 3 5 1
2 4 5 6
1 2 3

Sample Output 2

Hint

$1\leq n\leq 10^5，0\leq a_i\leq 10^6$。

$1\leq m\leq 5×10^4$，$t=1\ or\ 2$。

$1\leq l_i\leq r_i\leq n$，$1\leq x_i\leq 10^6$。

区间的异或难以维护。

我们可以把所有的数拆成二进制的，那么由数据范围可知，每个数的二进制位数不超过20位，我们可以建20棵线段树。

每一棵线段树维护区间取反，$0→1$或$1→0$；区间求和。

所以用一个标记即可解决。

时间复杂度为$O(nklogn)$，$k$为二进制转化的位数，即所需线段树个数，$k\leq20$。

Code

#include<bits/stdc++.h>
using namespace std;
int read()
{
	int x = 0, w = 0;
	char ch = 0;
	while (!isdigit(ch)) {w |= ch == '-'; ch = getchar();}
	while (isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();}
	return w ? -x : x;
}
const int N=100010;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
int n,m;
struct seg_tree
{
	int s,Xor;
}t[N<<2][22];
void pushdown(int root,int len,int bit)
{
	if(!t[root][bit].Xor) return;
	t[root<<1][bit].s=(len-(len>>1))-t[root<<1][bit].s;
	t[root<<1|1][bit].s=(len>>1)-t[root<<1|1][bit].s;
	t[root<<1][bit].Xor^=1,t[root<<1|1][bit].Xor^=1;
	t[root][bit].Xor=0;
}
void pushup(int root,int bit)
{
	t[root][bit].s=t[root<<1][bit].s+t[root<<1|1][bit].s;
}
void change(int root,int l,int r,int ll,int rr,int bit)
{
	if(ll<=l&&r<=rr)
	{
		t[root][bit].Xor^=1;
		t[root][bit].s=(r-l+1)-t[root][bit].s;
		return;
	}
	pushdown(root,r-l+1,bit);
	int mid=l+r>>1;
	if(ll<=mid) change(root<<1,l,mid,ll,rr,bit);
	if(rr>mid) change(root<<1|1,mid+1,r,ll,rr,bit);
	pushup(root,bit);
}
int query(int root,int l,int r,int ll,int rr,int bit)
{
	if(ll<=l&&r<=rr) return t[root][bit].s;
	pushdown(root,r-l+1,bit);
	int mid=l+r>>1,tot=0;
	if(ll<=mid) tot+=query(root<<1,l,mid,ll,rr,bit);
	if(rr>mid) tot+=query(root<<1|1,mid+1,r,ll,rr,bit);
	return tot;
}
int main(int argc, char const *argv[])
{
	n=read();
	for(int i=1;i<=n;++i)
	{
		int x=read();
		for(int j=0;j<=20;++j)
			if((1<<j)&x) change(1,1,n,i,i,j);
	}
	m=read();
	while(m--)
	{
		int type=read();
		if(type==1)
		{
			long long ans=0;
			int l=read(),r=read();
			for(int i=20;~i;--i)
				ans=(ans<<1)+query(1,1,n,l,r,i);
			cout<<ans<<endl;
		}
		else
		{
			int l=read(),r=read(),x=read();
			for(int i=0;i<=20;++i)
				if((1<<i)&x) change(1,1,n,l,r,i);
		}
	}
	return 0;
}